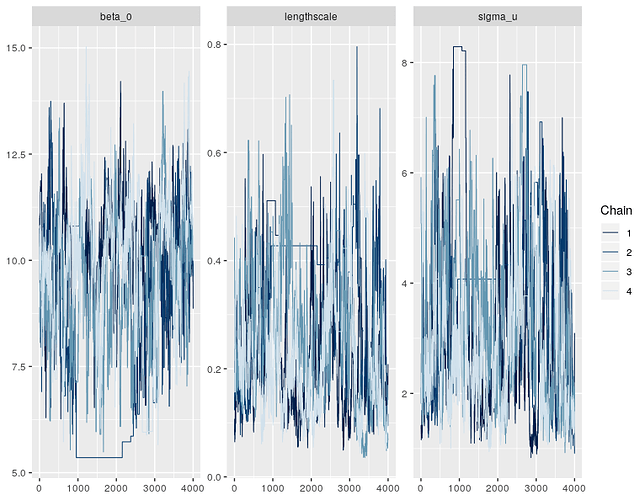
Right, it looks like the posterior for this model has an awkward geometry, so the sampler is getting a bit stuck in some points. This isn’t very surprising for GP models - there’s often some non-identifiability in the parameters, e.g. between the lengthscale and variance components. Or between the GP and the intercept.
Two options here, the most general one first, then a GP-specific one second:
Option 1. tune the sampler
You can make the sampler more effective (less correlated) by increasing the number of leapfrog steps, L. Unlike NUTS (Stan’s default sampler), the HMC algorithm in greta doesn’t tune L, so the user has to specify it. The default value (uniformly sampling L between 5 and 10) works well for models with simple geometry, but probably needs to be increased here. Try:
draws1 <- mcmc(
m1,
hmc(Lmin = 20, Lmax = 25),
one_by_one = TRUE
)
Note that more leapfrog steps implies more evaluations of the posterior density and its gradient, so will take longer to run. Try doubling Lmin and setting Lmax = Lmin + 5, until you get a good trade-off between speed and number of effective samples (see coda::effectiveSize()), the number of effective samples per second is probably the metric you want to look at.
It’s annoying to have to do this tuning for models like this. There’s a development branch of greta that implements NUTS (using a development version of tensorflow probability), though for annoying computational reasons it’s less effective than HMC on less-complicated models. I have a plan to implement tuning of this parameter during warmup, but it’s not trivial and not very high on my to do list. A simple thing we could do quickly (after NUTS is ready to be released in greta) is implement a self-tuning HMC that runs NUTS during warmup, records the distribution of leapfrog steps it takes, then uses that number of leapfrog steps during sampling with vanilla HMC. But manual tuning of L is the most practical solution for now.
BTW, I gave the experimental NUTS sampler a go on this model, and it didn’t do quite as well as vanilla HMC with the L parameters I suggested above.
Option 2. marginalise the intercept
The ML approach to Gaussian processes has some nice features, like the ability to create new kernels by adding and multiplying other kernels. Ie. adding functions together, which implies adding together the resulting variance covariance matrices. See the kernel cookbook for some nice illustrations and explanations.
greta.gp supports this approach to designing GP kernels, so you can define something crazy - like a linear regression with (smoothly) temporally-varying coefficients, plus a spatial random effect - in 5 lines:
n <- 100
x <- cbind(temp = rnorm(n),
rain = runif(10),
time = seq_len(n),
lat = runif(n),
lon = runif(n))
environmental <- bias(1) + linear(c(5, 5), columns = 1:2)
temporal <- expo(100, 1, columns = 3)
spatial <- mat32(c(3, 3), 1, columns = c(4:5))
K <- environmental * temporal + spatial
eta <- gp(x, K)
you can also pull out the separate components of this GP, by projecting it using only one of the component kernels
eta_time <- project(eta, x, temporal)
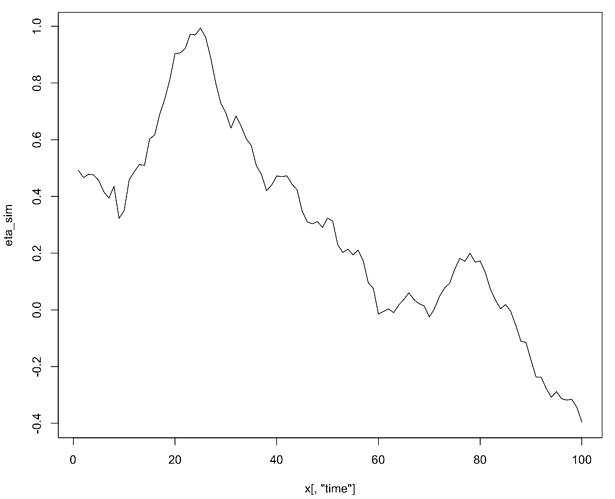
E.g. to fit a model (in this case just the prior) and plot just the temporal effects (which gets multiplied by the environmental linear model) you would do:
m <- model(eta)
draws <- mcmc(m)
eta_time_draws <- calculate(eta_time, draws)
eta_sim <- as.matrix(eta_time_draws)[100, ]
plot(eta_sim ~ x[, "time"], type = "l")
Sorry, that got a bit involved and off topic. Been a while since I played with compositional GPs and got excited.
The interesting thing here though is if you represent an intercept (with normal prior) in the GP ( via the bias() kernel above), it marginalises that parameter. The intercept is a priori Gaussian, and the GP results are a priori Gaussian, so it can combine their variances to get a Gaussian distribution over their sum. That means you don’t need to explicitly model beta_0 at all, it’s taken care of by the GP. You can do:
# beta_0 <- normal(0, 5)
sigma_e <- cauchy(0, 1, truncation = c(0, Inf))
sigma_u <- cauchy(0, 1, truncation = c(0, Inf))
lengthscale <- normal(0, 10, truncation = c(0, Inf))
k1 <- mat32(lengthscale, sigma_u ^ 2)
k2 <- bias(25) # pass in the prior variance on beta_0 (5 ^ 2)
K <- k1 + k2
f_gp <- gp(pts, K, tol = 1e-6)
f <- f_gp # + beta_0
distribution(y1) <- normal(f, sigma_e)
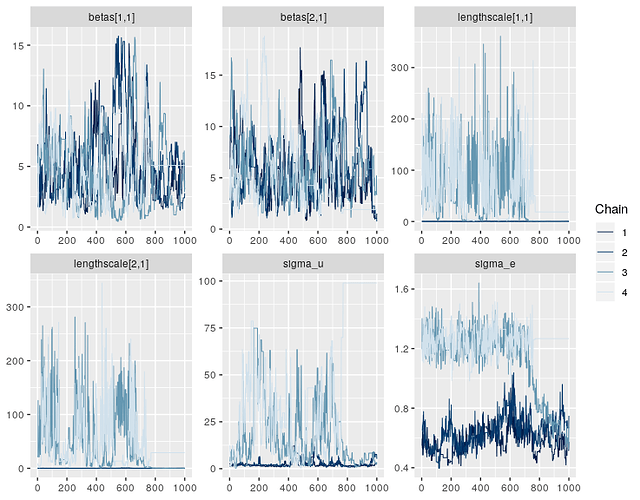
m1 <- model(lengthscale, sigma_u)
draws1 <- mcmc(m1, one_by_one = TRUE)
This samples much more nicely, because the geometry is less wacky. You can do the same trick for linear components in the model with the linear kernel.
To extract samples of beta_0 you can do:
beta_0 <- project(f, pts, k2)[1]
beta_0_draws <- calculate(beta_0, draws1)
GPs are magical.
Option 3. Do both.
Using the bias kernel approach, and increasing L a bit would probably be a good idea