Hi all,
Good question, @Marc!
These types of operations are a little bit tricky, because of the need for the likelihood of the model to be differentiable with with respect to the model parameters - so that you can do HMC. That’s the same limitation in Stan. And I’ve only seen examples of the Stan ternary operator working on data, not on parameters, and in the change point model @hrlai linked above, they don’t use the ternary operator - they do the maths to explicitly marginalise it.
As a design principle, we don’t want greta to let users do something that would result in an incorrect model, so introducing a general ternary-like operator might be tricky.
In your specific case, it would be possible to get tensorflow to return a differentiable function. I’ve pasted some tensorflow code below, that uses TF v1 (like the current greta release), and uses a nice tfautograph function that makes tf$case() work like dplyr’s case_when(). When you differentiate this, it returns a piecewise derivative. So that would be a valid model that we could sample with HMC.
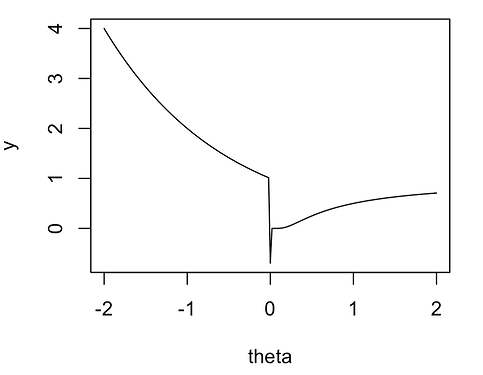
However it may not sample well at all. for one thing, it’s unlikely that theta would every be close enough to 0 (within double precision float rounding error) to evaluate the second case, but there’s a discontinuity around 0 that might really trip up HMC. It will have a lot of trouble sampling around that region, because it’s expecting to be moving around a fairly smooth space. The HMC leapfrogs steps will keep jumping over the discontinuity and not sample it correctly. That will also be the case for any other generic MCMC algorithm too. To illustrate what I mean, here’s a plot of the function you described, with x = 0, and theta in -2 to 2 (note that I removed a minus sign because I think the third condition will otherwise always return NAs):
x <- 0.5
theta <- c(
seq(-2, 0, length.out = 100), 0, seq(0, 2, length.out = 100)
)
y <- dplyr::case_when(
theta < 0 ~ x^theta,
theta == 0 ~ log(x),
TRUE ~ (x)^(1/theta)
)
plot(y ~ theta, type = "l")
You could probably change this model so that the function doesn’t have sharp discontinuities, but in general, providing an operator like this to greta will expose people to running into these kinds of problems. I don’t think it would be feasible to code it in such a way that we could warn users about that either. So I’m a little unsure whether it would be a good idea to put that functionality into greta.
Maybe we should look in more depth at what options Stan provides for sampling here, since they have obviously though about this problem a lot?
tf$case gradient check code:
# load greta first to make sure we have the right TF loaded
library(greta)
library(tensorflow)
library(tfautograph)
# TF1 style code execution
sess <- tf$Session()
# x is data, theta is a parameter
x <- as_tensor(0.5, dtype = tf$float64)
theta <- tf$placeholder(dtype = tf$float64)
# this is tfautograph's nicer interface to tf$case
y <- tf_case(
theta < 0 ~ x ^ theta,
theta == 0 ~ log(x),
default = ~ x ^ (1 / theta)
)
# check we can evaluate the result
sess$run(y, feed_dict = dict(theta = -2))
[1] 4
sess$run(y, feed_dict = dict(theta = 2))
[1] 0.7071068
sess$run(y, feed_dict = dict(theta = 0))
[1] -0.6931472
# now more importantly, check we can create and evaluate the gradient
grad_y <- tf$gradients(y, theta)[[1]]
grad_y
Tensor("gradients/AddN:0", dtype=float64)
sess$run(grad_y, feed_dict = dict(theta = -2))
[1] -2.772589
sess$run(grad_y, feed_dict = dict(theta = 0))
[1] 0
sess$run(grad_y, feed_dict = dict(theta = 2))
[1] 0.1225323
note this does not work with tf$cond - no gradient is returned